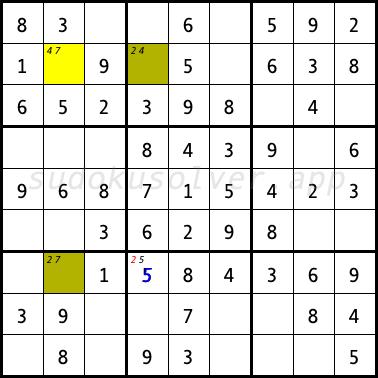
XY-Wing

The XY-Wing technique uses three cells and three candidates marked X, Y and Z to analyze the chain. One cell (pivot) has exactly two candidates X and Y, the other cell (pincer 1) that "sees" the pivot, has exactly two candidates Y and Z, the third cell (pincer 2), which also "sees" the pivot, has exactly two candidates X and Z. If the pivot has the value X, then the pincer 2 will have the value Z. If the pivot has the value Y, then pincer 1 1 will have the value Z. Thus, from the cells that "see" both pincers at the same time, we can remove the value of Z.

In the sudoku diagram below, the XY-Wing is formed by the R3C3 cell (pivot) and the R1C1 and R3C4 cells (pincers). The pivot R3C3 can have two digits 3 and 6. If it gets the digit 3, then the cell R3C4 will have the digit 5. However, if the pivot R3C3 has the value 6, then the cell R1C1 will have the digit 5. So from the cells that simultaneously "see" the cells R1C1 and R3C4 we can delete the candidate 5, i.e. from the cells R1C4, R1C6 and R3C2. With this elimination, in the R1C6 cell the only digit 4 can only be placed.



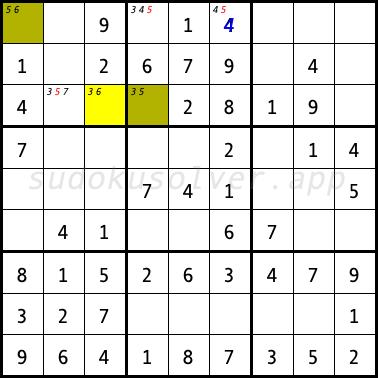
In the next sudoku diagram, the XY-Wing is formed by the cells R2C2, R2C4 and R7C2 (X = 4, Y = 7, Z = 2). Thus, you can remove the candidate 2 from the R7C4 cell. You can place the digit 5 in this cell.