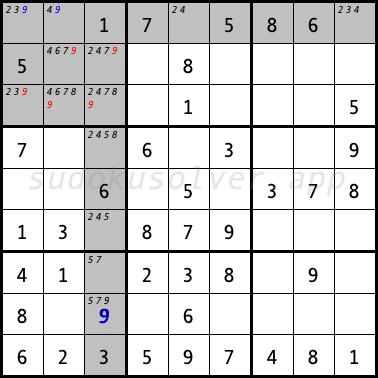
Locked Candidate

A Locked Candidate occurs when a given digit might be placed in a house (column, row, box) only at the intersection with another house. In this situation, you can eliminate this digit from the remaining cells of the second house.

In the sudoku diagram below, in the right middle box, the digit 2 might only be entered in the cells R4C7 and R6C7 (two marked in blue), which are also in the seventh column. Thus, we can eliminate the digit 2 from the remaining cells of this column, i.e. from the cell R7C7 (2 marked in red). Thanks to this elimination, we can only place the digit 7 in the R7C7 cell.



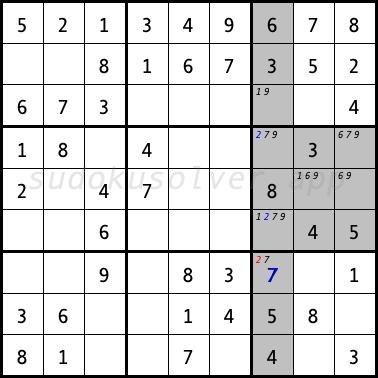
In the next sudoku diagram, the digit 9 in the first row might only be placed in the R1C1 and R1C2 cells, which also belong to the upper left box. We can therefore eliminate the digit 9 from the remaining cells of this box. Looking at the third column, we can see that we can only enter the digit 9 in the cell R8C3 because it has been eliminated from tbe cells R2C3 and R3C3.