Almost Locked Set

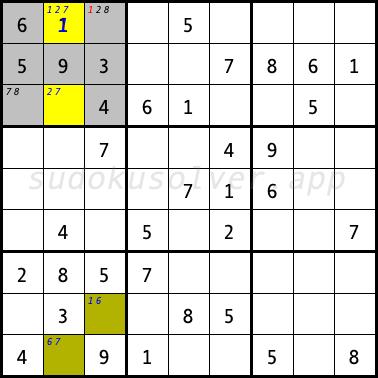
An Almost Locked Set occurs when exactly N + 1 digits are candidates in N cells of a given house. The smallest almost locked set almost is a cell with two candidates. A single almost locked set does not allow any eliminations. One technique using two almost locked sets is ALS-XZ. To use this technique, there must be a digit X that cannot occur simultaneously in both sets. Thus, if the digit X is placed in one of the sets, the other will automatically become an naked set. So if there is a digit Z that appears in both sets, then you can eliminate this digit from the cells that "see" all the cells of both sets containing the digit Z, because either the first set will contain this digit, or the second set will contain this digit, or both.

In the sudoku diagram below, you can place the three digits 1, 2 and 7 in the cells of the upper left box R1C2 and R3C2. This is the first almost locked set. In the cells of the lower left box R8C3 and R9C2 you can place the three digits 1, 6 and 7. This is the second almost locked set. The digit 7 is a digit X because it cannot occur simultaneously in both sets. The digit 1 is a digit Z, which appears in both sets. Using this technique, the digit 1 can be eliminated from the cell R1C3, this cell sees all the cells of the both sets containing the digit 1. Thanks to this elimination, the digit 1 in the upper left box can only be placed in the cell R1C2.



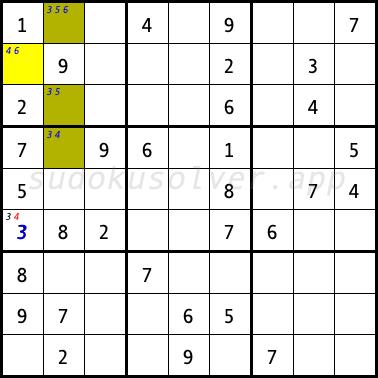
In the next sudoku diagram, in the R2C1 cell there is a pair of candidating digits 4 and 6. This is the first almost locked set. In the cells of the second column R1C2, R3C2 and R4C2 there are four candidates 3, 4, 5 and 6. This is the second almost locked set. The digit 6 is a digit X because it cannot occur simultaneously in both sets. The digit 4 is a digit Z, which appears in both sets. Using this technique, the digit 4 is eliminated from the R6C1 cell, this cell can see all the cells of the both sets containing the digit 4. Thanks to this elimination, only the digit 3 can be placed in the R6C1 cell.